The Missing Millions in Maps: Exploring Causes of Uncertainties in Global Gridded Population Datasets
Citation: Kuffer M, Owusu M, Oliveira L, Sliuzas R, van Rijn F. The Missing Millions in Maps: Exploring Causes of Uncertainties in Global Gridded Population Datasets. ISPRS International Journal of Geo-Information. 2022; 11(7):403. https://doi.org/10.3390/ijgi11070403
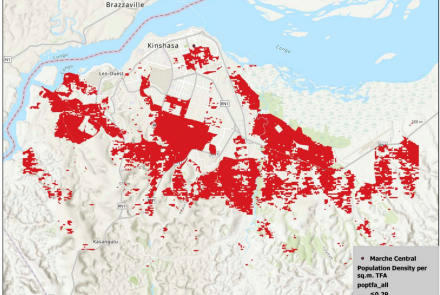
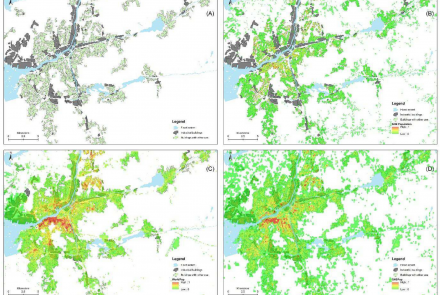
Abstract: Gridded population datasets model the population at a relatively high spatial and temporal granularity by reallocating official population data from irregular administrative units to regular grids (e.g., 1 km grid cells). Such population data are vital for understanding human–environmental relationships and responding to many socioeconomic and environmental problems. We analyzed one very broadly used gridded population layer (GHS-POP) to assess its capacity to capture the distribution of population counts in several urban areas, spread across the major world regions. This analysis was performed to assess its suitability for global population modelling. We acquired the most detailed local population data available for several cities and compared this with the GHS-POP layer. Results showed diverse error rates and degrees depending on the geographic context. In general, cities in High-Income (HIC) and Upper-Middle-Income Countries (UMIC) had fewer model errors as compared to cities in Low- and Middle-Income Countries (LMIC). On a global average, 75% of all urban spaces were wrongly estimated. Generally, in central mixed or non-residential areas, the population was overestimated, while in high-density residential areas (e.g., informal areas and high-rise areas), the population was underestimated. Moreover, high model uncertainties were found in low-density or sparsely populated outskirts of cities. These geographic patterns of errors should be well understood when using population models as an input for urban growth models, as they introduce geographic biases.